
Find The Total Area Of The Shaded Regions Y X Sqrt 36 X 2 Study Com
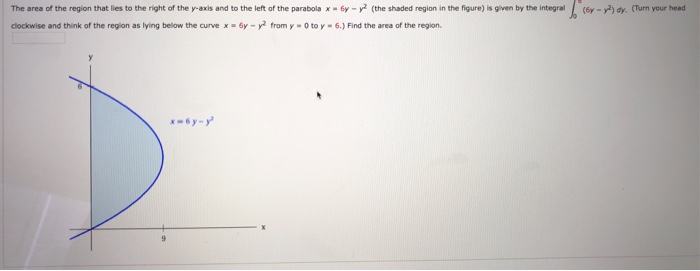
Given equation of the parabola is y 2=8x a=2The endpoints of its latus rectum are (a,2a) and (a,−2a)Points are (2,4) and (2,−4)Area of the triangle Δ 1 = ∣∣∣∣∣∣∣∣ 0522 24−4 111 ∣∣∣∣∣∣∣∣ =6The equation of the tangent at (2,4) is given by y=x2(1)equation of the tangent at (2,−4) is given by −y=x2(2)and the equation of the tangent at (05,2) is given by y=2x1(3)Intersection pointsSee the answer See the answer See the answer done loading Let R be the region in the xy plane bounded between the parabola y=6−x^2 and the line y=−x Fill in the blanks to complete the integral so that it equals area of this region
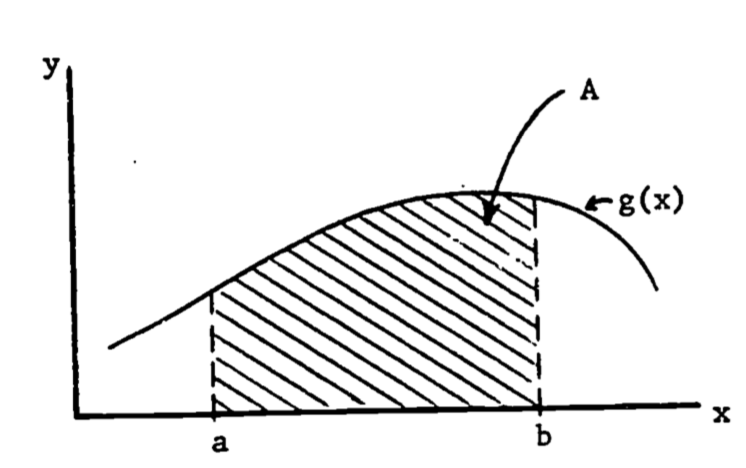
Consider the parabola y=x^2 the shaded area is
Consider the parabola y=x^2 the shaded area is-Sketch the region bounded by the curves y = x 2 2, y = x, x = 0 and x = 1 Also, find the area of this region Also, find the area of this region Advertisement Remove all ads (ii) Find the area enclosed between the Parabola y = x 2 and the straight line 2x – y 3 = 0 (March – 10) Answer Question 2 Find the area enclosed between the curve x 2 = 4y and the line x = 4y – 2 (March 11) Answer Question 3 (i) Area of the shaded portion in the figure is equal to (ii) Consider the curves y = x 2, x = 0, y = 1, y = 4
How Do You Find The Area Between The Curves Y 4x X 2 And Y X Socratic
Consider the parabola (y 1)2 = 2(x 1) Which equation is used to find the directrix?`x^(2) y^(2) le 100 rarr "inside of a circle"` `sin(xy) gt 0` `x y in (x,pi) uu (2pi,3pi)""` `x y = c rarr "equation of a line"` required area = shaded region `= 1/2 pi(10)^(2) = 50 pi`Now, the radius of the disk is simply given by y = x3, so V = Z 2 0 π(x3)2dx = π Z 2 0 x6dx = π x7 7 2 0 = π 128 7 −0 = 128π 7 39 Find the volume of the solid generated by revolving the region bounded by y = x2 and the line y = 1 about (a) the line y = 1 Answer Note that y = x2 and y = 1 intersect when x = ±1
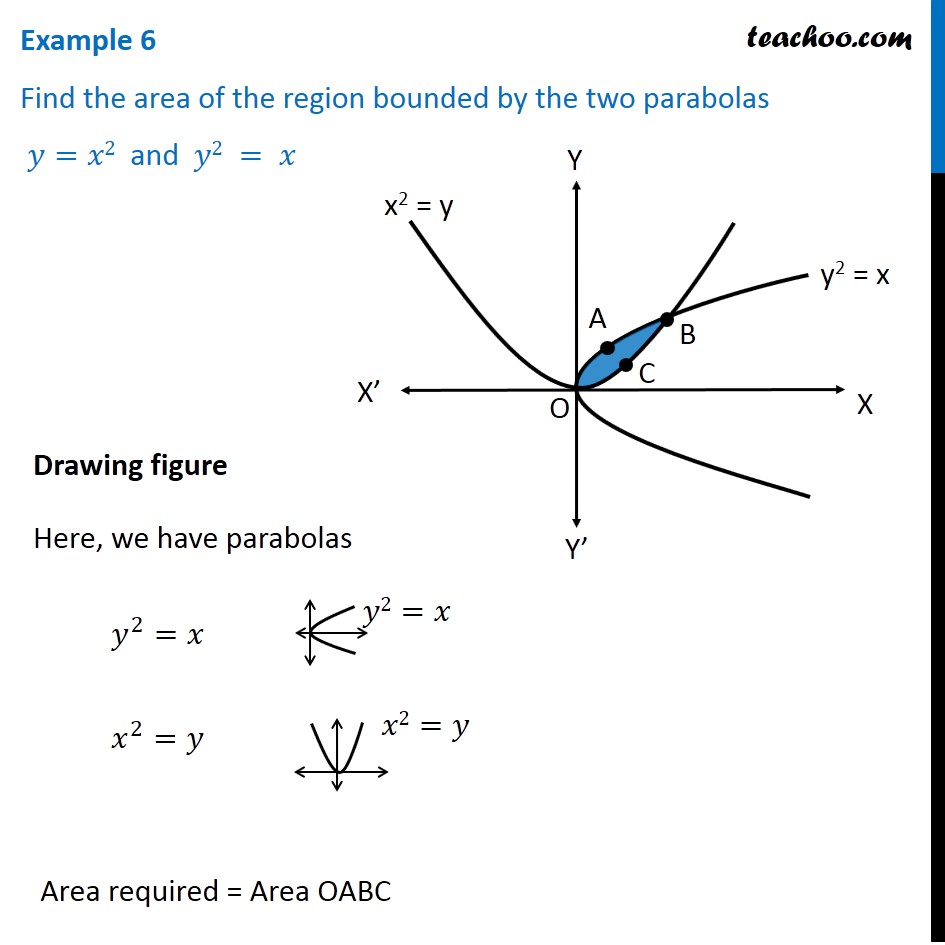
Draw the graph of the function y = x 2 and x = y 2 in a coordinate axes (2) Find the point of intersection of the above graphs (2) Find the area of the region bounded by the above two curves (2) Answer 1 The two function are parabolas as shown in the figure 2 We have, y = x 2 and x = y 2 x = (x 2) 2 ⇒ x – x 4 = 0 ⇒ x(1 – x 3) = 0The equation of the upper half of the sideways parabola is y = √ x and that of the lower half is y = − √ x The equation of the lower right hand boundary of the region is just y = x − 2 We find the area A between the two curves by integrating the difference between the top curve and the bottom curve in each regionTranslations of the basic parabola Vertical translation When we translate the parabola vertically upwards or downwards, the yvalue of each point on the basic parabola is increased or decreasedThus, for example, translating the parabola upwards by 9 units, shifts the general point (a, a 2) to (a, a 2 9)The equation of this new parabola is thus y = x 2 9
Consider the parabola y=x^2 the shaded area isのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 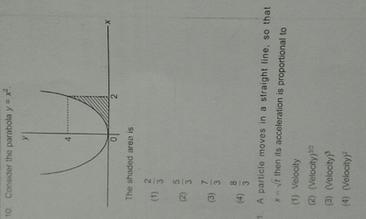 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 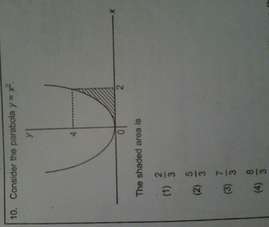 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 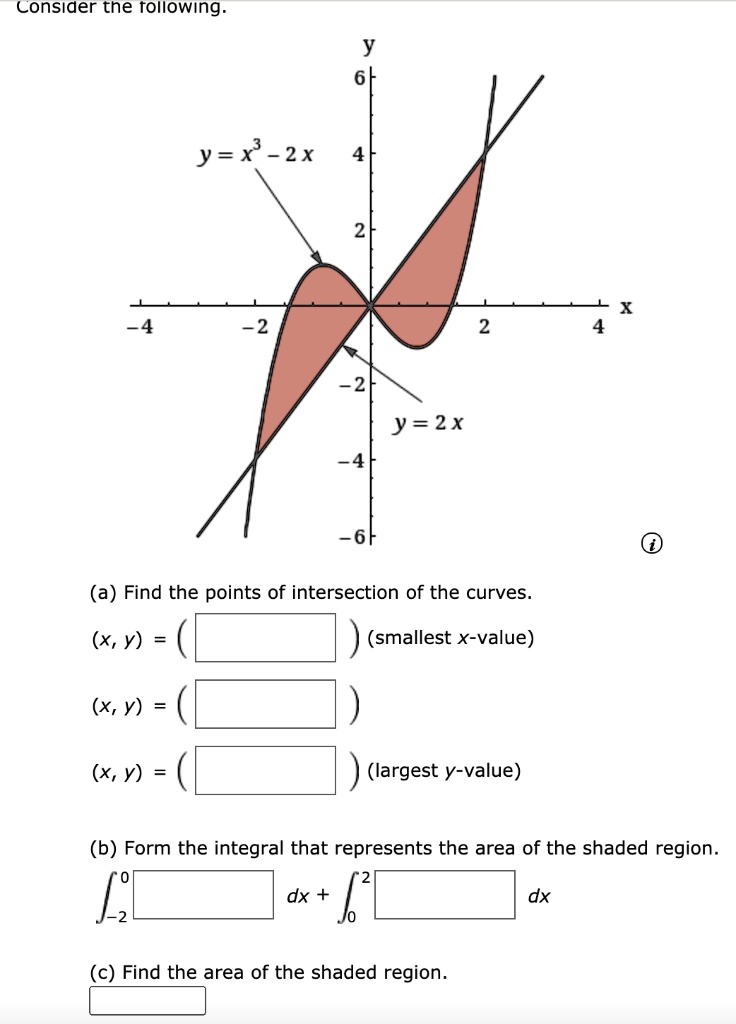 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 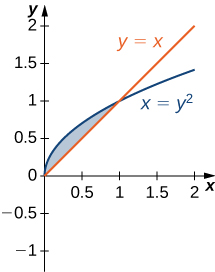 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 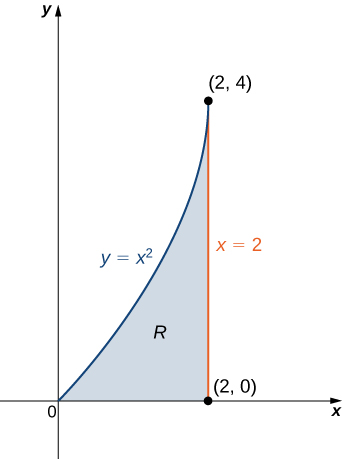 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 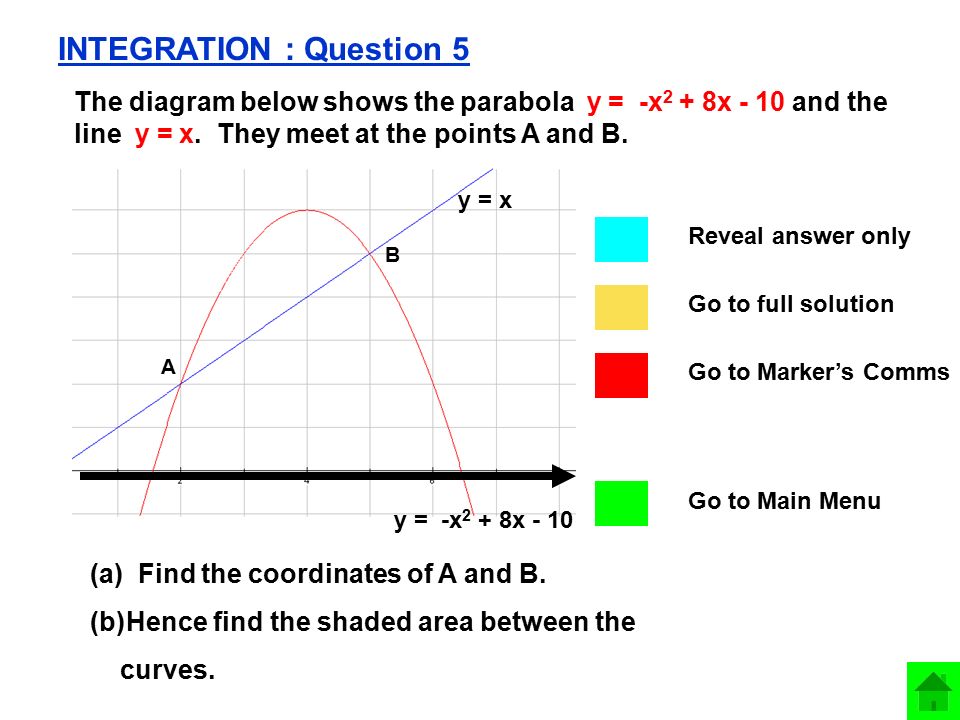 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 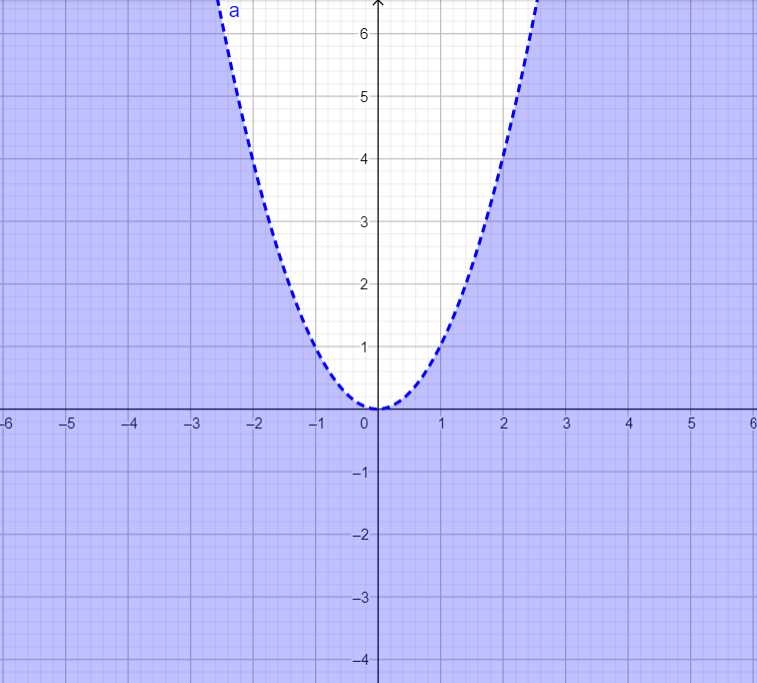 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 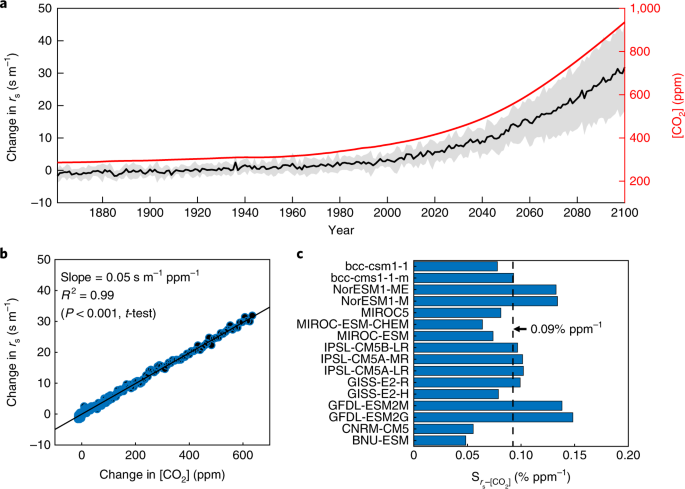 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 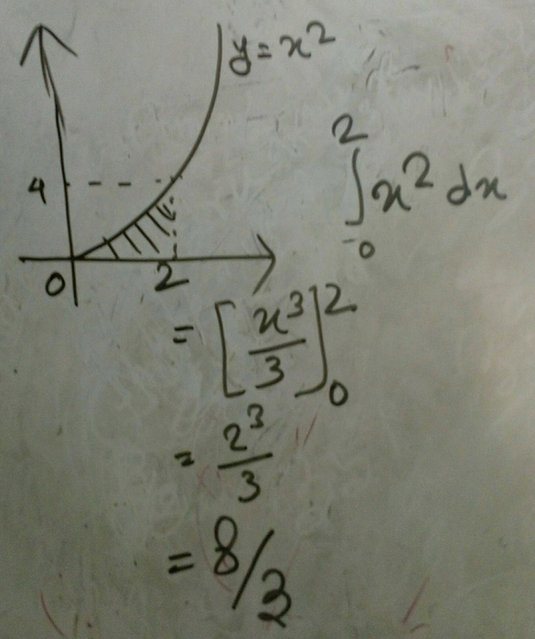 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
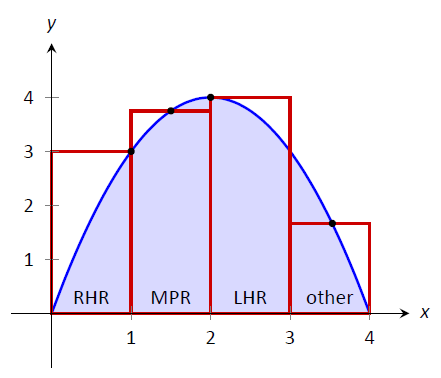 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 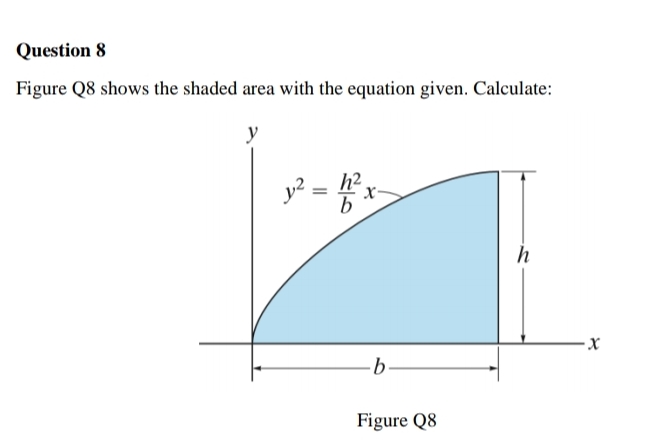 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 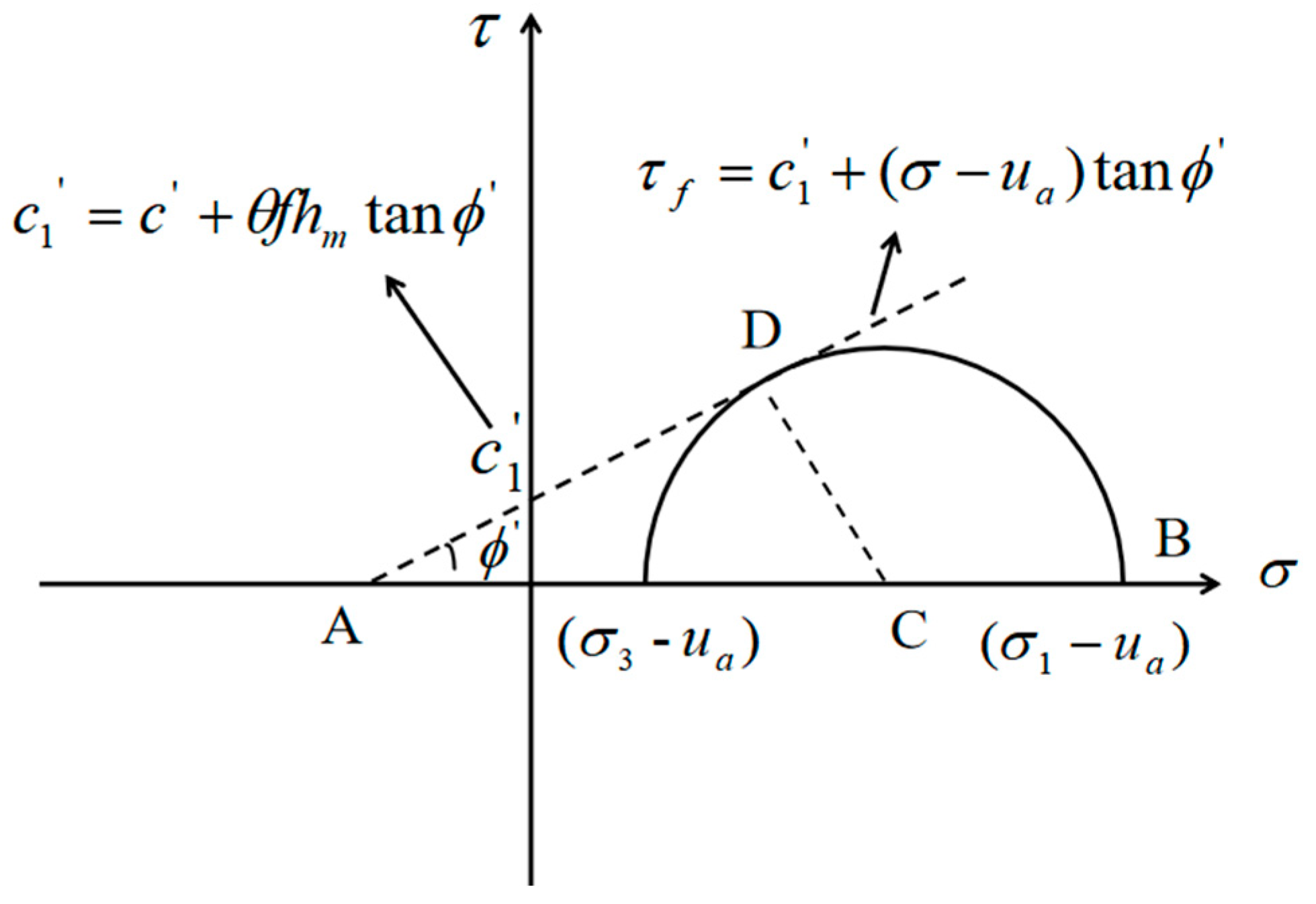 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 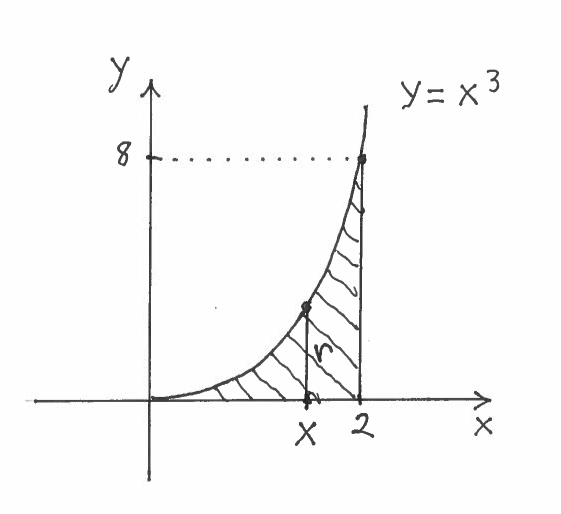 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 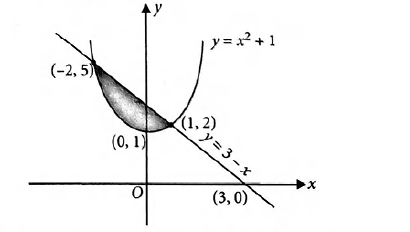 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 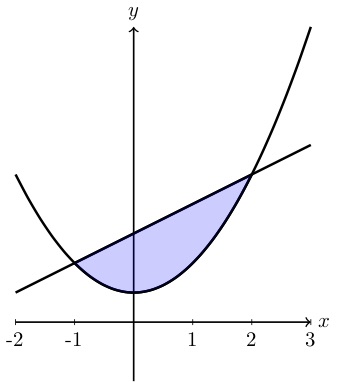 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 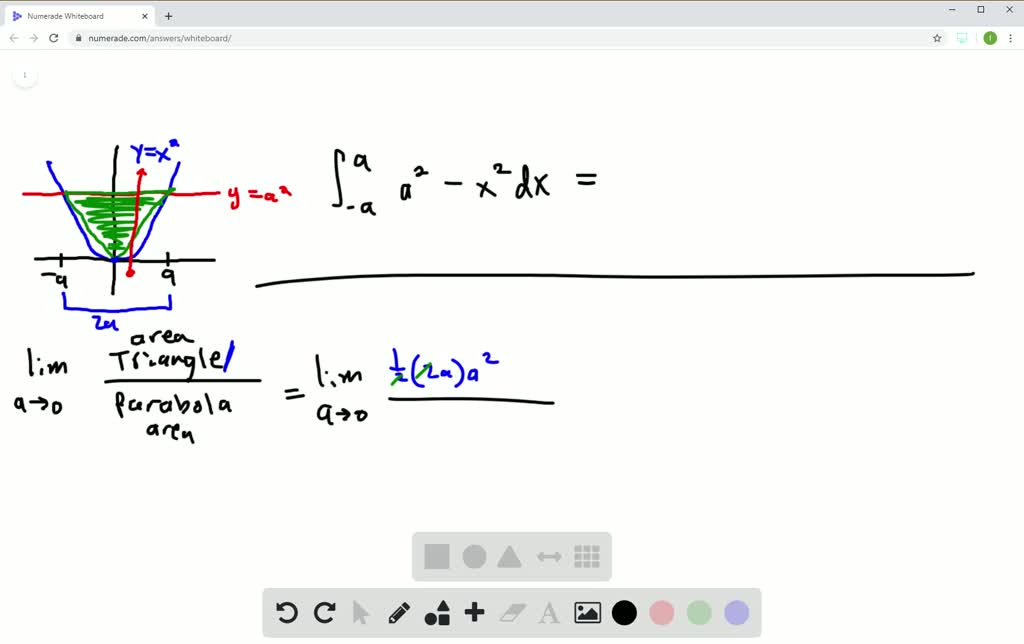 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 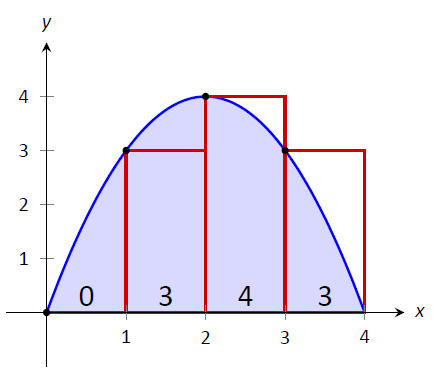 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 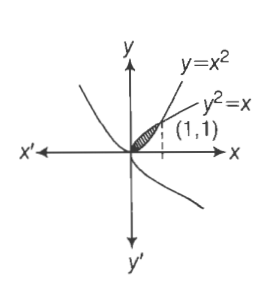 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | 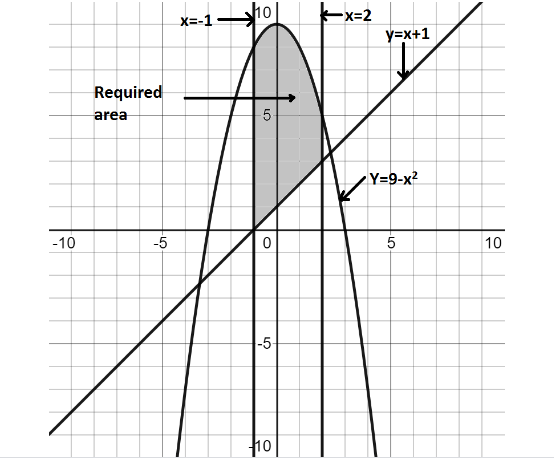 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |  Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
「Consider the parabola y=x^2 the shaded area is」の画像ギャラリー、詳細は各画像をクリックしてください。
 Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of | Solved The Figure Here Shows Triangle A O C Inscribed In The Region Cut From The Parabola Y X 2 By The Line Y A 2 Find The Limit Of The Ratio Of The Area Of |
What is the center of a circle represented by the equation (x9)2 (y−6)2=102?9 Find the area of the region bounded by the parabola y = x^2 and y= xarea of region bounded,area of a bounded region,area of the region bounded by the gr
Incoming Term: consider the parabola y=x^2 the shaded area is, 19.consider the parabola y=x^(2) quad the shaded area is,



